Opto-thermal actuation:

Doubly clamped beams are driven into out-of-plane limit cycle oscillations interferometrically. The 205 nm thick device layer is supported on 400 nm thick silicon dioxide and forms a Fabry-Perot interference cavity with the substrate underneath. Continuous-wave laser at a wavelength of 633 nm causes thermal expansion of the beams. The absorption-gap relation with a negative slope results in constant amplitude limit cycle oscillations in the system.

       

Understanding the Causes of LCO:

It is known that thermally induced limit cycle oscillations are driven by coupling between heating and displacement, and yet a simple beam theory model of a doubly supported beam subject to centerline heating shows no displacement until buckling. In order to understand the thermal-mechanica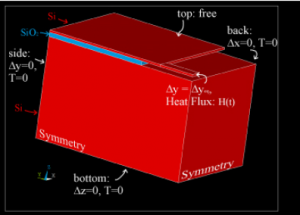l coupling in our beams, we built and Finite Element Method (FEM) model of a doubly supported beam subject to centerline heating. The model showed that displacement due to heating is caused by asymmetry of the support which leads to a phenomenon known as “imperfection buckling.”

Analysis of Model Equations:

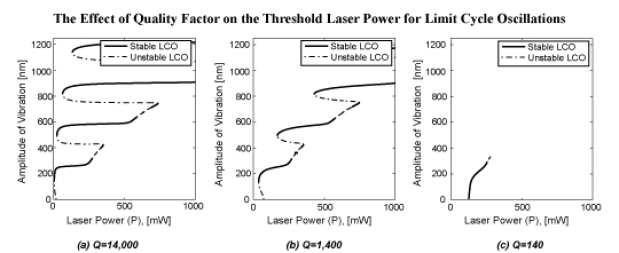
We model the temperature and displacement of these thermally actuated beams using coupled non-linear differential equations and use a numerical continuation software package, AUTO2000, to analyze the equilibrium (i.e. static deflection) solutions and stable periodic (i.e. limit cycle) solutions. Analysis of the equations suggests that periodicity in the interference field should lead to multiple limit cycle oscillations with periodically spaced amplitudes. Such models also allow us to predict the threshold power for self-oscillation.

Limit Cycle Oscillation and Entrainment:

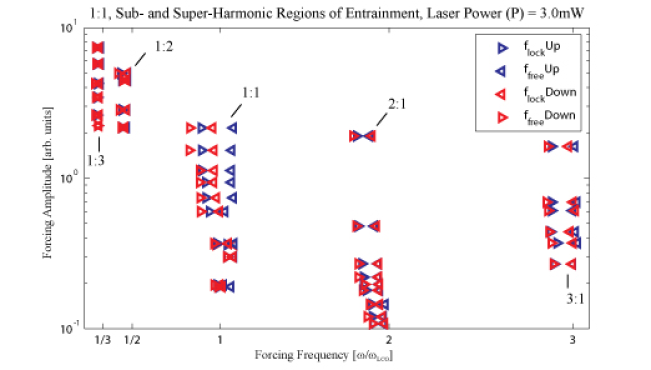
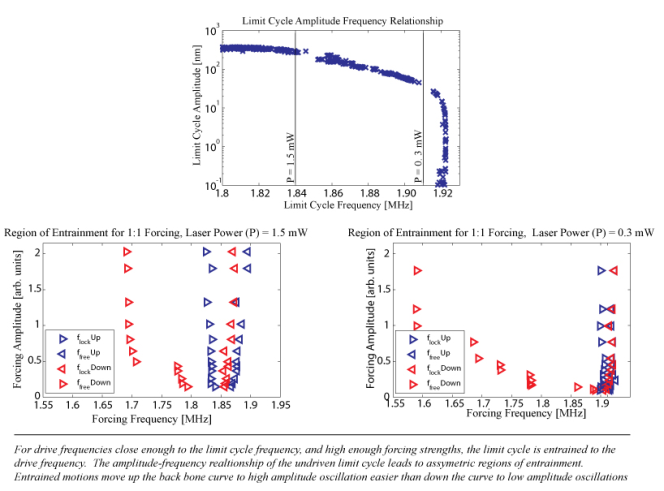
For high laser power, we can entrain the limit cycle by inertially driving the beam. In addition to 1:1 entrainment we observe sub-harmonic entrainment of order 2:1 up to 7:1 as well as super-harmonic entrainment of orders 1:2 and 1:3. We find that when entrained, the amplitude of response follows the backbone curve, and that the asymmetry of this curve leads to asymmetry of the regions of entrainment. To our knowledge sub- and super-harmonic entrainments of this order have not been previously observed in MEMS. Sub- and super-harmonic entrainment could be used for signal division or multiplication.

Acknowledgements

This work is supported by the National Science Foundation under Grant Number CMMI-1634664. The experimental work was performed in part at the Cornell NanoScale Facility, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (Grant NNCI-2025233). The numerical work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI- 1548562. Specifically, it used the Bridges-2 system, which is supported by NSF award number ACI-1928147, at the Pittsburgh Supercomputing Center (PSC). This work also made use of the Cornell Center for Materials Research Shared Facilities which are supported through the NSF MRSEC program (DMR-1719875).